Eigenvalue problem with Physics-informed Neural Network

Solve eigenvalue-eigenfunction pair with PINNs

Eigenvalue problem

We consider the eigenvalue problem of the general form

\[\mathcal{L} u = \lambda ru\]

where \(\mathcal{L}\) is a given general differential operator, \(r\) is a given weight function. The unknown variables in this problem are the eigenvalue \(\lambda\), and the corresponding eigenfunction \(u\).

PDEs (sometimes ODEs) are always coupled with necessary boundary conditions, whether numerical ones (Dirichlet, Neumann, Robin), or what Boyd calls “natural” ones (function being periodic, or regular or finite at boundaries, etc.). For eigenvalue problems, homogeneous numerical boundary conditions are numerically “consistent” boundary conditions, in that these BCs really lead to matrix eigenvalue problems in FEM or spectral methods. The non-homogeneous BCs seem to be physically well defined, but incur extra vectors in the linear system that cannot be merged to an eigenvalue problem (see also [[Numerics of 1D torsional oscillation]]); thus I am at lost how to implement them. Finally, natural boundary conditions are almost always implicitly satisfied. For instance, periodicity is inherently satisfied by using Fourier basis in spectral methods, and almost all numerical methods only allow finite/regular solutions (it might be possible to choose a set of basis functions with singularities, but I am not sure about the implications).

Conventional numerical solvers for eigenvalue problem

Two conventional numerical approaches are discussed in [[Numerics of 1D torsional oscillation]], namely finite-element method (FEM) and spectral method. Both methods use basis expansion to discretize the system (or its weak form, in FEM and Galerkin-spectral method), and the eigenvalue problem of differential operators is reduced to solving a matrix eigenvalue problem.


Physics-informed neural network

Consider an arbitrary differential equation of the form

\[\mathcal{L}(u) = 0,\qquad x\in\Omega\]

with boundary condition

\[F(u)|_{\partial \Omega} = 0.\]

Unlike the operator in eigenvalue problem, now the operator \(\mathcal{L}\) here includes all fields, including the forcing terms. It is also not necessarily linear. Another approach to solving such PDEs is to build the surrogate solution via a neural network

\[\hat{u}(x) = f(x;\theta)\]

where \(\theta\) denotes the collective of neural network parameters. The task is then to train the network, optimize on the parameters, to seek a good approximate \(f(\cdot, \hat{\theta})\) of the true \(u^*(\cdot)\). There are different ways to construct the optimization problem. In particular, physics-informed neural network (PINN, Rassi et al. 2019) suggests the objective function be formed by penalizing the combined loss of PDE residual and the boundary discrepancy

\[L(\theta) = \lambda_\mathrm{int} \sum_{x_i\in D_\mathrm{int}} L[\mathcal{L}f(x;\theta)|_{x_i}] + \lambda_\mathrm{BC} \sum_{x_i\in D_\mathrm{BC}} L[F(f(x_i;\theta))]\]

where \(L[\cdot]\) is point-wise measure of the loss. For instance, one can take the \(\ell^2\) norm, so that \(L[y] = y^2\) for every scalar \(y\). Therefore, except for at the boundary where the values are known, the PDE loss and the objective function does not require any further knowledge of the solution. This is why PINN is generally considered unsupervised learning.

Applications and variants

The aforementioned framework is just the most simple (however general) framework for PINNs. One of the many merits of PINNs is that the optimization stage can be easily made compatible with inverse problems, and the approximate forward field can be trained together with the underlying model parameters. For further info, see Cuomo et al., 2022.


Eigenvalue problem with PINNs

We return to the eigenvalue problem with the form \(\mathcal{L}u = \lambda r u\) in the beginning. Solving the eigenvalue problem is slightly different from the aforementioned framework, because

  • In eigenvalue problem, both the eigenvalue and eigenfunction (i.e. the eigenpair) are sought, not just the solution field;
  • Eigenvalue problem typically contains a bunch of eigenpairs, usually even infinitely many (but in most system relevant to physics, numerably infinitely many, so the eigenvalues are quantized). Therefore, the PINN for eigenvalue problem should
  • simultaneously optimize on the eigenvalue and the eigenfunction;
  • can have additional DOF as to which eigenvalue to search for.

For eigenvalue discovery, a typical approach is to build a network alongside an optimizable scalar value as the eigenvalue, and optimize on both.

\[L(\theta, \lambda) = \lambda_\mathrm{int} \sum_{x_i\in D_\mathrm{int}} L[\mathcal{L}f(x;\theta)|_{x_i} - \lambda r(x_i)f(x_i;\theta)] + \lambda_\mathrm{BC} \sum_{x_i\in D_\mathrm{BC}} L[F(f(x_i;\theta))]\]

This approach is used in Jin et al. 2022, Cornell et al. 2022. Another, more exotic method, is to use the variational form with Rayleigh-quotient (Kovacs et al., 2022).

For multiple eigenvalue discovery, Jin et al. 2022 suggests two approaches: either add an additional “driving” term \(e^{-\lambda + c}\), and progressively increase \(c\), to drive the neural network to search for larger eigenvalues, or add an orthogonal condition, so that the new eigenfunction sought should be orthogonal to the pre-existing eigenfunctions. The former now requires extra ad hoc choices, while the latter only works when the eigenfunctions are known to be orthogonal, e.g. for Hermitian operators, and the computational expense for evaluating orthogonality increases for higher eigenvalues.

There is one other problem concerning eigenvalue problems - the system always has trivial solutions, i.e. \(u\equiv 0\), arbitrary \(\lambda\). There are also different proposals as to how to avoid the trivial solution. Jin et al., 2020 proposes penalizing on \(1/\lambda^2\) and \(1/u^2\); similarly, Jin et al. 2022 introduces the norm loss. I use the norm loss, which takes the form

\[L_\mathrm{norm}(\theta, \lambda) = \left[1 - \left(\frac{1}{|D_\mathrm{int}|}\sum_{x_i\in D_\mathrm{int}} f(x;\theta)^p \right)^{1/p}\right]^2.\]

The most natural choice is \(p=2\). This will try to find the eigenfunction that is normalized (in the \(p\)-norm sense) to 1.

Example 1: standing wave

The classical textbook eigenvalue problem is described by the following Sturm-Liouville problem

\[\left\{\begin{aligned} &\frac{\partial^2 u}{\partial x^2} = \lambda u,\quad x \in (0, 1) \\ &u|_{x=0,1} = 0 \end{aligned}\right.\]

which has eigenvalues and eigenfunctions

\[\lambda_k = (k\pi)^2,\quad u_k = \sin k\pi x,\quad k \in \mathbb{N} \quad \Longrightarrow \quad u_k = \sqrt{2} \sin k\pi x.\]

The latter \(u\) is the eigenfunction with normalized norm, i.e. \(\int u_k^2 dx = 1\).

Example 2:

The eigenvalue problem is given by the Legendre differential equation

\[\mathcal{L}u = \lambda u,\qquad \mathcal{L}u = \frac{d}{dx}\left[(1 - x^2)\frac{du}{dx}\right] = (1 - x^2) \frac{d^2 u}{dx^2} - 2x \frac{du}{dx},\qquad x \in (-1, 1)\]

There is no explicit (or as Boyd puts it, “numerical”) boundary condition to this problem; instead, the mere requirement of the solution being regular and finite at endpoints is sufficient to yield quantized eigenvalues.

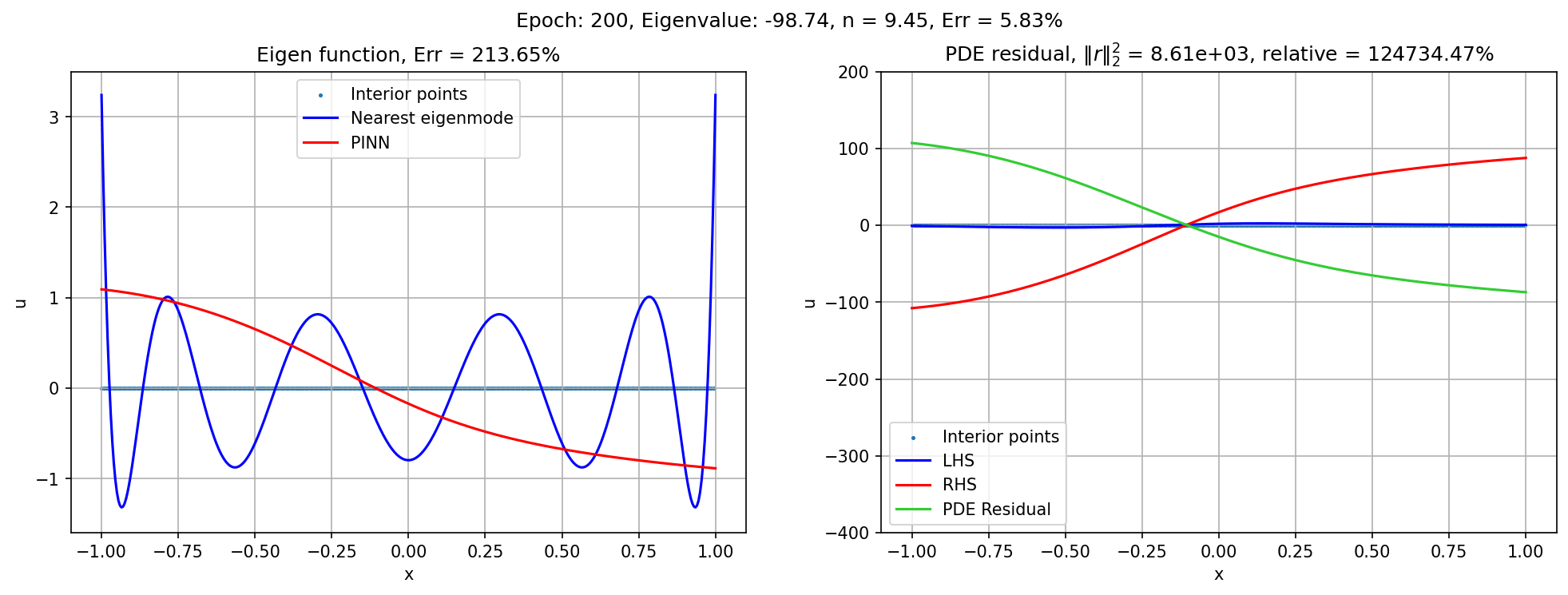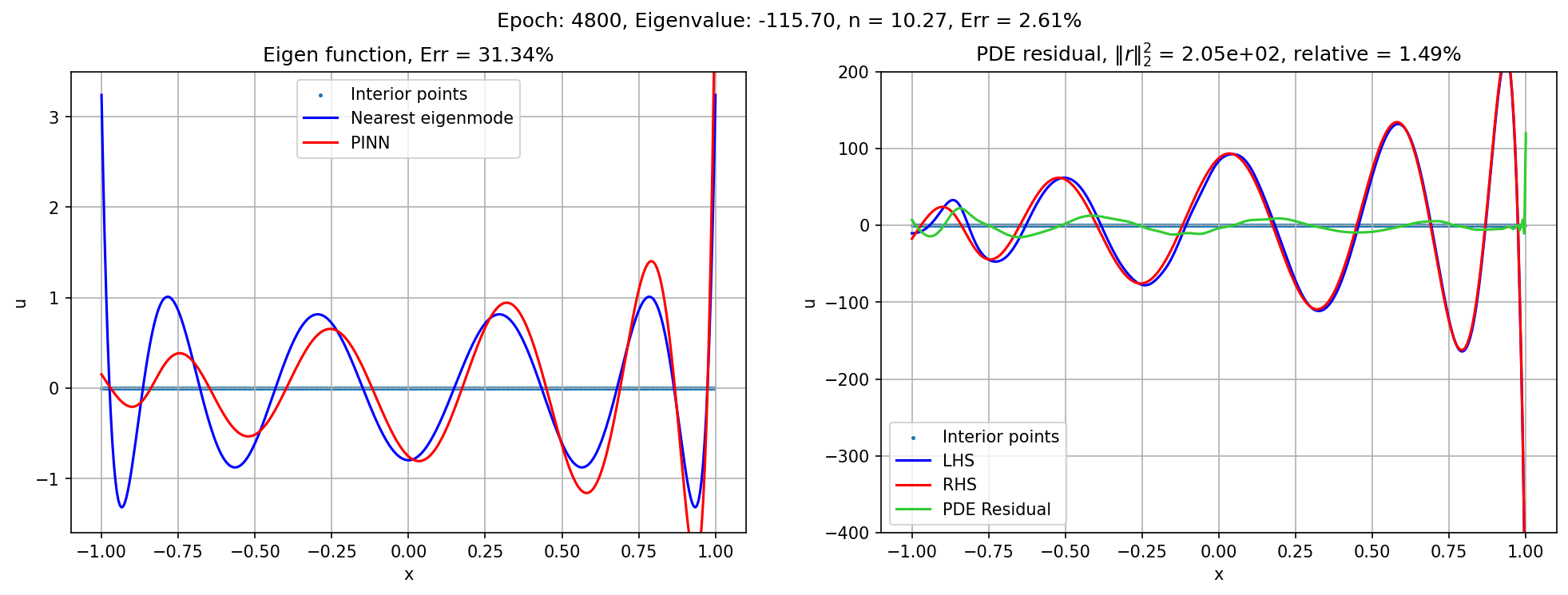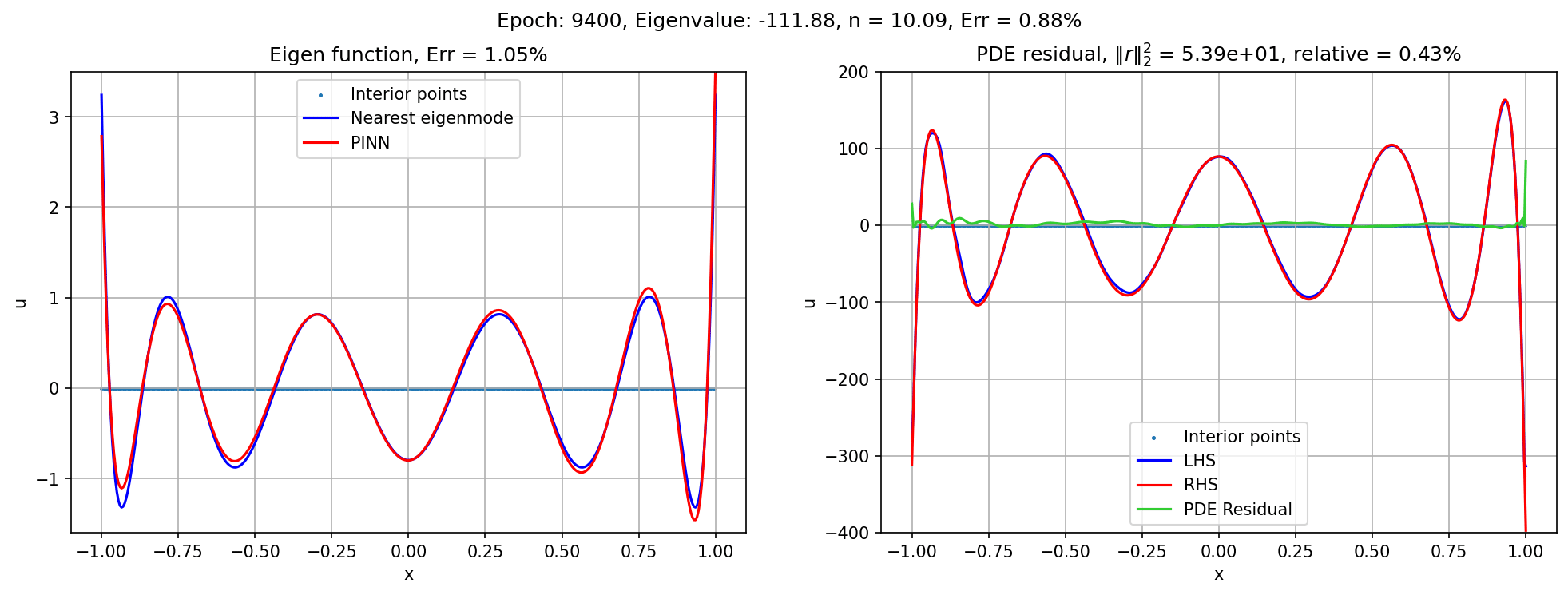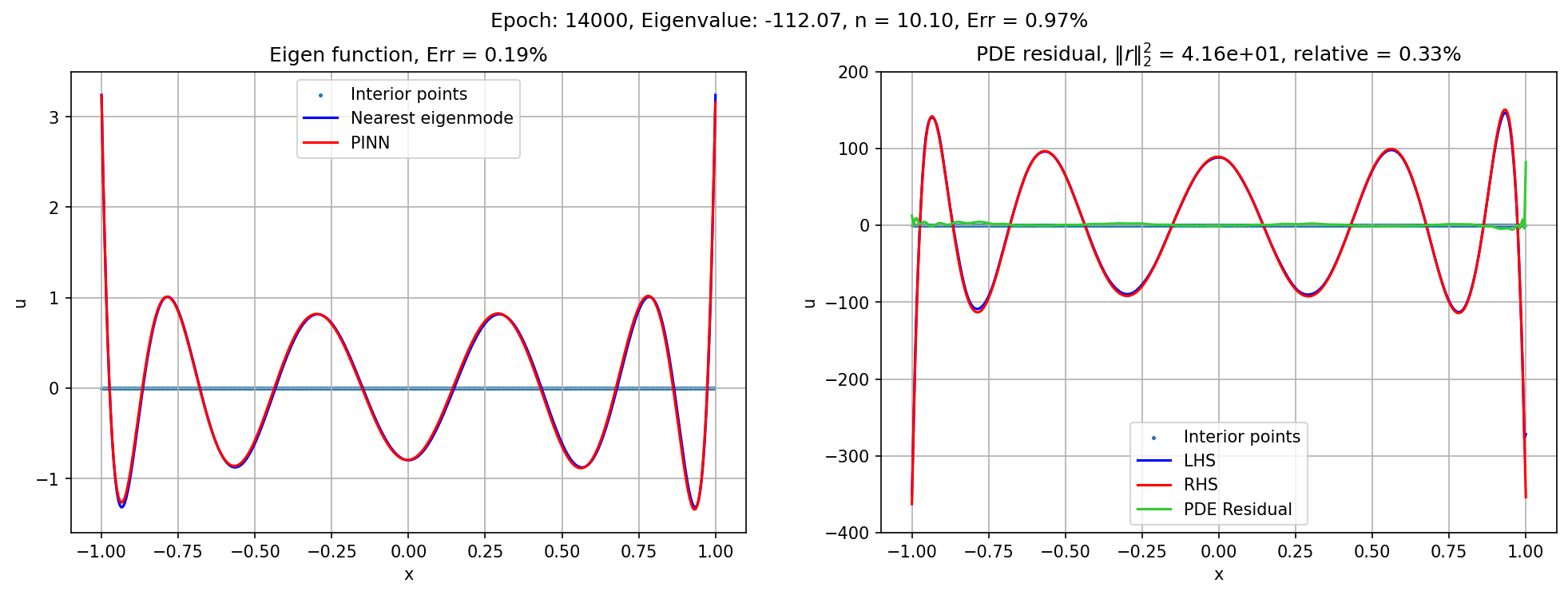
Eigenvalue-eigenfunction searching for Legendre equation, with driver c set to 100. The target solution it converges to is the normalized Legendre polynomial of degree 10, and the eigenvalue -n(n+1)=-110.


FAQ

Here I summarize the frequently-asked-questions (asked by myself) and the tricks that worked, as well as the intuition behind.

  • Stagnating eigenvalue. I usually initialize \(\lambda = c\). It is often the case when \(c\) is far away from the actual \(\lambda^*\), the eigenvalue will stagnate near \(c\) and refuse to go further. This typically happens in training neural networks because of the strong nonlinearity of the functional space. When the solution is far from optimal, it is necessary for the neural network to have strong enough momentum in order to explore the topography of the loss function. In this case, the gradient w.r.t. \(\lambda\) is usually too small for \(\lambda\) to vary significantly.
    • Solution: Fine-tune the driver term in the form \(e^{(-\lambda + c)/\alpha}\). \(\alpha\) is a scaling factor, and shows the estimated magnitude of \(\lambda^* - c\). For instance, in the standing wave problem, when searching for \(k=7\) solution, which has an eigenvalue of \(480\), and the \(c\) is set to be \(400\), then if one uses the original form, i.e. \(\alpha = 1\), the driver term already has too small a gradient at \(\lambda = 405\). At this stage \(\lambda\) cannot go further. If however, one estimate the distance to be \(\sim 10\), and use \(\alpha=10\) or \(20\), the method usually works.
  • Spurious eigenfunctions. When searching for high-frequency eigenfunctions, the network sometimes converges to a spurious solution, with several pieces of solution get wielded together. Therefore, the solution satisfies the eigenvalue problem piece-wise, and at the junction forms a narrow spike in its derivatives. Since the spike is narrow, the contribution to the PDE loss is still small, therefore the training loss may still seem ideal. In particular, the network can have zero solution on part of the function, wielded with another part of the approximately true solution. This is favorable for the neural network because low-frequency trivial solution is much easier to construct.
    • Solution: increase number of interior points. As the interior points increase, the network has to go for sharper, narrow spikes to achieve the same training loss, which ultimately outweighs the cost of finding the actual smooth eigenfunction.
  • Zero solution: the symptom is characterized by zero solution or very small amplitude solution, with the magnitude loss \(L_\mathrm{norm}\) platforms early on at \(1\).
    • Solution: this means the norm penalty just isn’t strong enough. Increase the regularization usually solves the problem.