How similar are random vectors in high dimensions?
Given two random vectors in high-dimensional space, how similar are they expected to be?
Consider two random vectors in high-dimensional space, how are their angular separation distributed? Do they tend to be more “similar”, or less “similar”, at high dimensions? This is the small question I want to address here.
The motivation comes from comparing vectors that are solutions to PDEs discretized using spectral method. The solution can be considered “converged” when the solution vectors “align” at different resolutions (different dimensions). A simple way to measure this “alignment”, or “similarity”, is to calculate the angular separation between the two vectors, or the inner product of the two normalized vectors, defined as
\[\cos < \mathbf{a},\mathbf{b} > = \frac{\langle \mathbf{a}, \mathbf{b} \rangle}{\|\mathbf{a}\|\|\mathbf{b}\|} = \frac{\mathbf{a}^\top \mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}\]but then comes the problem: do I need to adjust my criterion for “good” alignment? If \(\cos < \mathbf{a},\mathbf{b} > = 0.99\) when \(\mathbf{a},\mathbf{b} \in \mathbb{R}^3\), it is somewhat good alignment. If the same inner product \(\cos < \mathbf{a},\mathbf{b} > = 0.99\) occurs for , say \(\mathbf{a},\mathbf{b} \in \mathbb{R}^{100}\), is it as good, worse, or better? In other words, if I get two random vectors in a 3-dimensional and an 100-dimensional space, are the odds that they align at \(\cos < \mathbf{a},\mathbf{b} > = 0.99\) different?
Preparation: surface of \(n\)-sphere, band element
I use the terminology that an \(n\)-sphere is an \(n\)-dimensional manifold, embedded in an \(n+1\)-Euclidean space, formed by points with equal distance to the origin. Therefore, points \(\pm R\) on the real axis is a \(0\)-sphere, a circle is a \(1\)-sphere, a (normal) sphere is a \(2\)-sphere.
To begin, we first need the surface of a unit \(n\)-sphere, which I shall denote as \(S_n\). The surface of an \(n\)-sphere with radius \(R\) is then \(S_n R^n\). There are simpler derivations available, but let us look at the brute-force method because as a mid-step, we can obtain the band-element on the unit \(n\)-sphere. For this purpose, let us look at the \(n\)-sphere as a series of \((n-1)\)-spheres (with varying radius) stacked in one dimension. For instance, a circle is a combination of two-point-segments (with varying segment length) combined in one direction, and a sphere is a combination of circles (with different radius) stacked in one direction. Following this logic, we can write \(S_n\) as
\[S_n = \int_{-1}^{+1} S_{n-1} r^{n-1} \frac{dx}{\sqrt{1 - x^2}}\]where the weight \((1 - x^2)^{-1/2}\) accounts for the slope of the surface, and \(r = \sqrt{1 - x^2}\) is the radius of the \((n-1)\)-sphere element at \(x\). Immediately this indicates that a “band-element”, or the surface area corresponding to \(dx\) at \(x\) is given by
\[dS_{n} = S_{n-1} r^{n-2} \, dx = S_{n-1} (1 - x^2)^{\frac{n-2}{2}} dx\]and the total area
\[S_n = \int dS_{n} = S_{n-1} \int_{-1}^1 (1 - x^2)^{\frac{n-2}{2}} \, dx = S_{n-1} I_{n-1}.\]Integral \(I_{n}\) can be calculated by standard trigonometric change of variables, integration by parts and establishing the recurrence relations. The process yields a simple close-form expression
\[I_{n} = \int_{-1}^1 (1 - x^2)^{\frac{n-1}{2}} dx = \int_0^\pi \sin^{n} \theta \, d\theta = \frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n+2}{2})} \sqrt{\pi}.\]Successive product of this integral cancels out most of the terms, leaving
\[\prod_{j=0}^n I_j = \pi^{\frac{n+1}{2}} \frac{\Gamma(\frac{1}{2})}{\Gamma(\frac{n+2}{2})} = \frac{\pi^{\frac{n+2}{2}}}{\Gamma(\frac{n+2}{2})}.\]In the end, we reach the expression for the surface area of the unit \(n\)-sphere
\[S_n = S_{n-1} I_{n-1} = S_0 \prod_{j=0}^{n-1} I_j = \frac{2\pi^{\frac{n+1}{2}}}{\Gamma(\frac{n+1}{2})}.\]Uniform distribution of vectors on unit \(n\)-sphere
For a normalized vector random variable \(\mathbf{x} \in \mathbb{R}^n\) , it is effectively an element of the unit \((n-1)\)-sphere, i.e. \(\mathbf{x} \in \mathbb{S}^{n-1}\). Uniform distribution on this unit \((n-1)\)-sphere is given by
\[p(\mathbf{x}) = S_{n-1}^{-1} = \frac{\Gamma(\frac{n}{2})}{2\pi^{\frac{n}{2}}}\]Vector \(\mathbf{x}\) that satisfy this distribution is denoted as \(\mathbf{x} \sim U(\mathbb{S}^{n-1})\). Due to isotropy, if a vector random variable \(\mathbf{x} \in \mathbb{R}^n\) is uniformly distributed in the complete space \(\mathbb{R}^n\) (\(\mathbf{x}\sim U(\mathbb{R}^n)\)) , then its normalization should follow \(p\), the uniform distribution on \(\mathbb{S}^{n-1}\). Thus \(p\) is the angular uniform distribution.
In the derivation above we obtained the band element, the surface area corresponding to \(dx\) in any direction. This turns out useful as it immediately yields the marginal distribution of the uniform distribution on \(\mathbb{S}^{n-1}\) in any direction:
\[p_i(x_i) = S_{n-2} (1 - x_i^2)^{\frac{n-3}{2}} \times S_{n-1}^{-1} = \pi^{-\frac{1}{2}} \frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})} (1 - x_i^2)^{\frac{n-3}{2}}\]Distribution of angular separation
Now it is time to return to the original problem. Given two random vectors in \(\mathbb{R}^n\) space, how is their angular separation distributed? Let us consider random vectors \(\mathbf{a},\mathbf{b} \in \mathbb{R}^n\). The goal is to characterize the distribution of the resulting random variable \(z=\langle \hat{\mathbf{a}}, \hat{\mathbf{b}} \rangle = \cos<\mathbf{a},\mathbf{b}>\).
For \(\mathbf{a},\mathbf{b} \sim U(\mathbb{R}^n)\) or \(\hat{\mathbf{a}}, \hat{\mathbf{b}} \sim U(\mathbb{S}^{n-1})\), the solution has now become quite simple thanks to the results from previous sections. Indeed, without loss of generality, we can always rotate the coordinate system such that axis \(x_1\) aligns with the first vector \(\mathbf{a}\). \(\hat{\mathbf{a}}\) then has coordinates \((1,0,\cdots)\). The inner product then becomes \(\langle \hat{\mathbf{a}}, \hat{\mathbf{b}} \rangle = \hat{b}_1\), i.e. the coordinate of \(\hat{\mathbf{b}}\) along this axis. The question is then essentially what is the distribution of \(\hat{b}_1\), given that \(\hat{\mathbf{b}} \sim U(\mathbb{S}^{n-1})\). This is nothing but the marginal distribution of any coordinate \(x_i\) obtained earlier, and hence
\[p(z) = p(\langle \hat{\mathbf{a}}, \hat{\mathbf{b}} \rangle) = \pi^{-\frac{1}{2}} \frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})} (1 - z^2)^{\frac{n-3}{2}}\]Or converted to the angle variable \(\theta = \arccos z\) ,
\[p(\theta) = p(z) \left|\frac{dz}{d\theta}\right| = \pi^{-\frac{1}{2}} \frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})} (\sin \theta)^{n-2}\]Now the conclusion becomes clear. When the vectors are uniformly distributed (whether in \(\mathbb{R}^n\) or on \(\mathbb{S}^{n-1}\)), neither the angular separation between the vectors nor the normalized inner product follows a uniform distribution in general. For both quantities, the distribution would get increasingly shifted towards an orthogonal state, i.e. \(z=\langle \hat{\mathbf{a}}, \hat{\mathbf{b}} \rangle = 0\) and \(\theta = \pi/2\). For \(p(\theta)\), all except the \(n=2\) case have angular separation more likely towards orthogonal state; at \(n=2\) (a circle), \(p(\theta)\) is constant across all angles. For \(p(z)\), all \(n > 3\) cases have angular separation more likely towards orthogonal state; at \(n=3\) (a sphere), \(p(z)\) is contant whereas at \(n=2\) (a circle), \(z\) is more likely to be \(\pm 1\) (aligned or anti-aligned). An illustration can be found below.
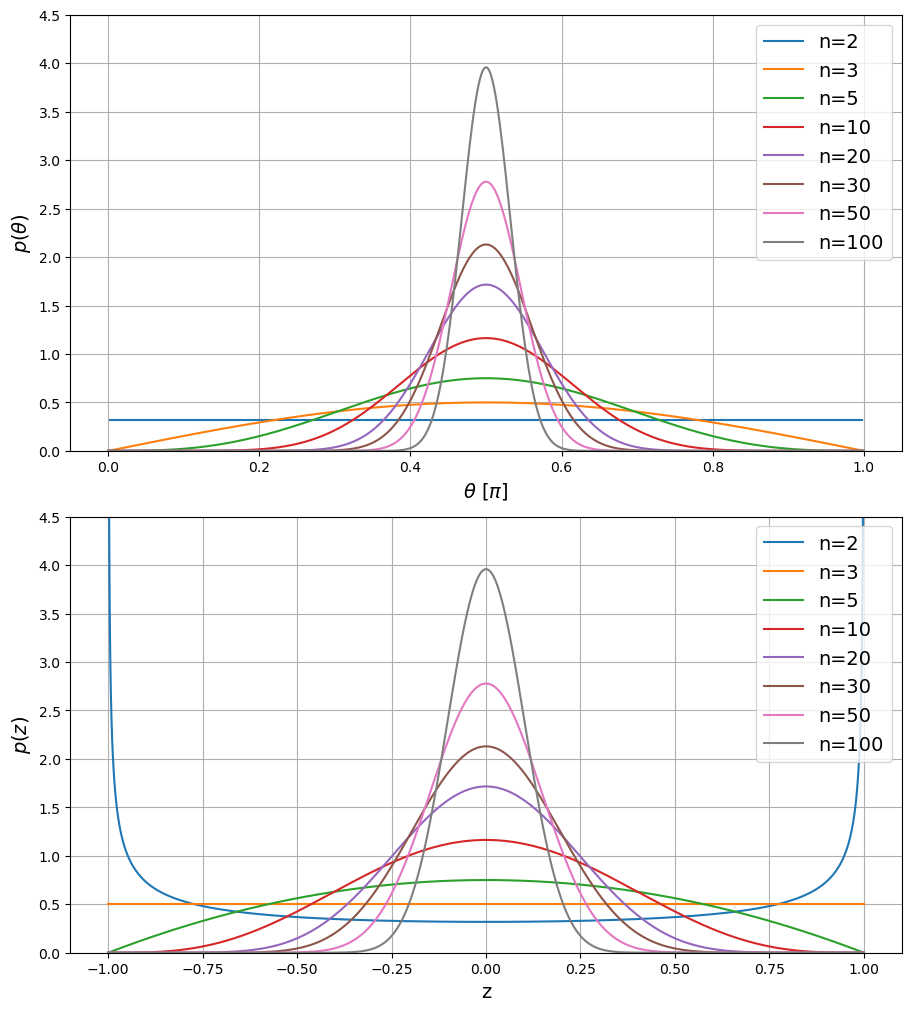
It is however worth mentioning that due to even symmetry with respect to \(z\) (or \(\theta = \pi/2\)), two random vectors on arbitrary \(n\)-sphere are always, on average, orthogonal. To be more precise, \(\forall n\),
\[\mathbb{E}_{\mathbf{a},\mathbf{b}\sim U(\mathbb{S}^{n})}[z] = \mathbb{E}_{\mathbf{a},\mathbf{b}\sim U(\mathbb{S}^{n})}[\langle \mathbf{a}, \mathbf{b} \rangle] \equiv 0,\quad \mathbb{E}_{\mathbf{a},\mathbf{b}\sim U(\mathbb{S}^{n})}[\theta] \equiv \frac{\pi}{2}.\]The variance and other moments can be computed accordingly, at least numerically. The variance decreases as \(n\) increases, as the distribution is increasingly shifted towards vectors being orthogonal.
Open question: generalization
A uniform distribution on an \(n\)-sphere \(U(\mathbb{S}^{n})\) is a special case of the von Mises-Fisher distribution, with concentration parameter \(\kappa = 0\). A natural further question is therefore, given two i.i.d. random vectors drawn from a general von Mises-Fisher distribution, what is the distribution of their angular separation \(\theta\), or their inner product \(z = \langle \mathbf{a}, \mathbf{b} \rangle\)?
This problem seems more challenging than the uniform distribution case, as a general von Mises-Fisher distribution has a mean direction, creating anisotropy. However, given the vast materials in statistics, and my relative ignorance, I very much expect a solution to have already been derived long ago. If this is the case, than what derived here might just be a special case.