Wave equation solver generated by New Bing
Despite not being a real hipster when it comes to latest technology, when MS Edge asked if I wanted to be on the waitlist for their AI-powered new Bing, I gladly agreed. Due to the existing rumors and demos using ChatGPT, I was indeed quite excited when I got the chance two days later to access their new Bing, and I had high expectations as well.
I tried to test its ability of combining code generation and physics/maths comprehension, so I asked it to generate a solver code in Python for wave equation. New Bing returned the following python code.
# Import numpy and matplotlib libraries
import numpy as np
import matplotlib.pyplot as plt
# Define the parameters of the wave equation
c = 1 # Wave speed
L = 10 # Domain length
T = 10 # Final time
nx = 101 # Number of grid points in space
nt = 101 # Number of grid points in time
dx = L / (nx - 1) # Spatial step size
dt = T / (nt - 1) # Temporal step size
# Check the stability condition
if c * dt / dx > 1:
print("The scheme is unstable. Please choose smaller dt or larger dx.")
exit()
# Define the initial condition function
def u0(x):
return np.exp(-10 * (x - L/2)**2)
# Define the boundary condition function
def g(t):
return 0
# Create the grid points in space and time
x = np.linspace(0, L, nx)
t = np.linspace(0, T, nt)
# Initialize the solution array with zeros
u = np.zeros((nt, nx))
# Apply the initial condition at t=0
u[0,:] = u0(x)
# Apply the boundary condition at x=0 and x=L for all t
u[:,0] = g(t)
u[:,-1] = g(t)
# Loop over the interior points and apply the finite difference scheme
for n in range(0, nt-1): # Time loop
for i in range(1, nx-1): # Space loop
u[n+1,i] = u[n,i] - c * dt / (2 * dx) * (u[n,i+1] - u[n,i-1]) + c**2 * dt**2 / (2 * dx**2) * (u[n,i+1] - 2 * u[n,i] + u[n,i-1])
# Plot the solution at different times using matplotlib animation
from matplotlib.animation import FuncAnimation
fig, ax = plt.subplots()
line, = ax.plot(x, u[0,:])
ax.set_xlim(0,L)
ax.set_ylim(-1.5,1.5)
ax.set_xlabel("x")
ax.set_ylabel("u")
ax.set_title("Wave equation solution")
def animate(n):
line.set_ydata(u[n,:])
return line
anim = FuncAnimation(fig, animate, frames=nt, interval=100)
plt.show()
This is an elegant piece of code, it has reasonable comments, good variable namings, and the entire structure is very much like a numerical modelling code. It also includes a nice animation snippet for visualization. It even safeguards the model with a condition on the CFL number.
The code is ready to run, and produces an animation as follows.
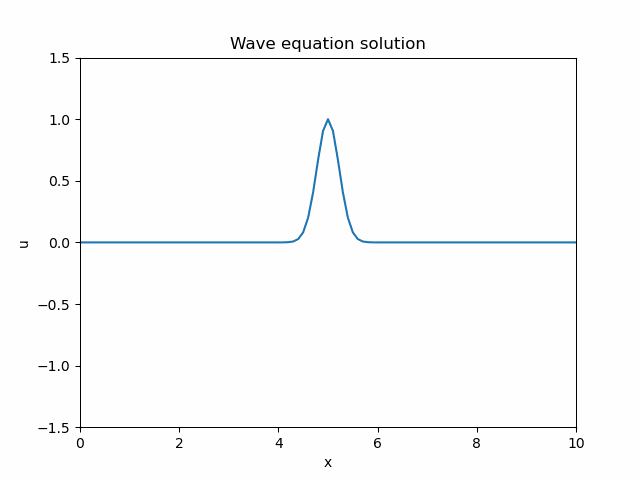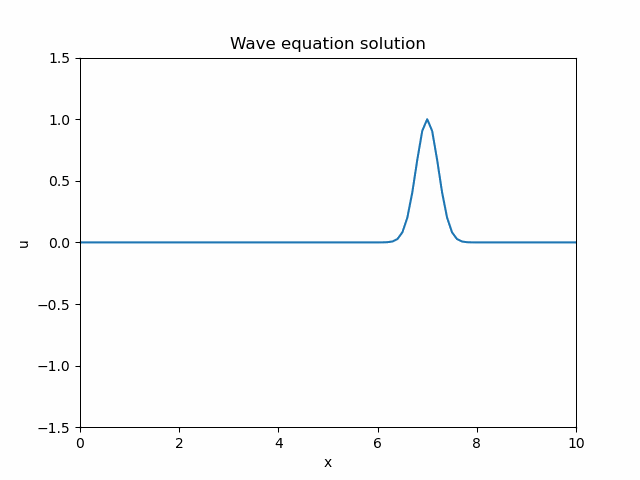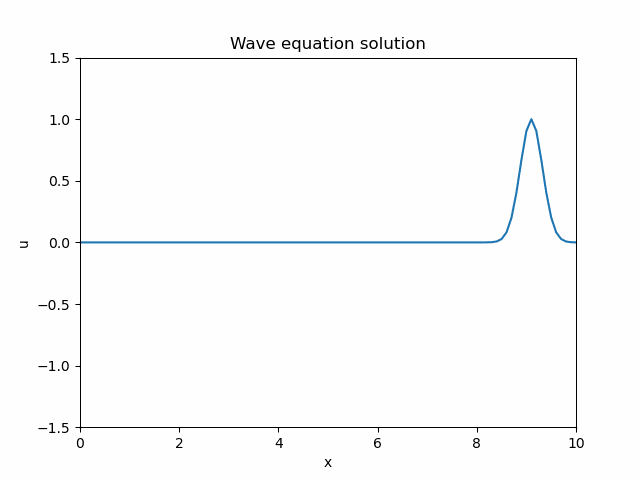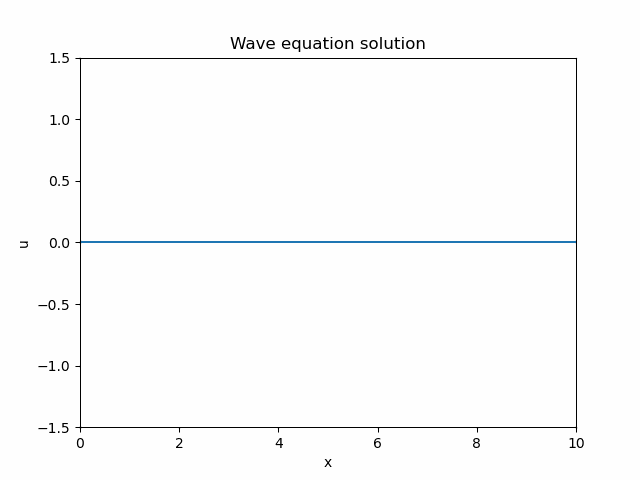
At first sight, it seems to be perfectly reasonable, even better than reasonable - there is no significant numerical diffusion, something unavoidable for finite difference schemes. But then, under closer inspection, two unexpected things emerge:
- As the wave packet reaches the boundary, there is no reflection.
- There is no left-travelling wave, only the right-travelling one.
For the first problem, I thought New Bing might have used an absorbing boundary, e.g. Gaussian tapering, PML, etc. As I checked the code, however, it was obvious that it only used homogeneous Dirichlet boundary condition. For the second issue, a possible explanation is that the code uses specific velocity initial conditions. However, the initial condition is also quite straightforward - only one initial condition on displacement.
My confusion spiralled after checking the code for five minutes, when I realized I didn’t even recognize the form of this “wave equation” time stepping scheme! This time stepper uses only the displacement field from the previous time step, hence only approximates a first-order time derivative in the equation:
# Loop over the interior points and apply the finite difference scheme
for n in range(0, nt-1): # Time loop
for i in range(1, nx-1): # Space loop
u[n+1,i] = u[n,i] - c * dt / (2 * dx) * (u[n,i+1] - u[n,i-1]) + c**2 * dt**2 / (2 * dx**2) * (u[n,i+1] - 2 * u[n,i] + u[n,i-1])
Writing down the formula on the white board, I came to the conclusion that this is simply not a wave equation. It seems to be some kind of advection-diffusion equation, which advects the packet to the right at velocity \(c\), and one with incorrect dimensions at that. It still seems a bit peculiar that the code is stable. Normally when a central difference is used that involves downstream/downwind grids, instability develops in the system. I attribute the stability to the diffusion term.
As a final attempt, I asked New Bing to explain the finite difference scheme used in the code. Its answer is as follows (maths contents prettified).
Sure. The finite difference scheme is a method to approximate the solution of a partial differential equation (PDE) such as the wave equation by discretizing the space and time domains into a grid of points and replacing the derivatives in the PDE by finite differences. For example, the wave equation in one dimension is:
\[u_{tt} = c^2 u_{xx}\]where u(x,t) is the displacement of the wave at position x and time t, and c is the wave speed. To apply the finite difference scheme, we introduce a uniform grid with spacing dx in space and dt in time:
\[x_i = i\, dx \quad \mathrm{for}\, i = 0, 1, \cdots, n_x - 1,\quad t_n = ndt \quad \mathrm{for}\, n = 0, 1, \cdots, n_t-1\]Then we denote \(u_i^n\) as an approximation of \(u(x_i,t_n)\) at the grid point \((x_i,t_n)\). The goal is to find \(u_i^n\) for all i and n using a recursive formula. To do that, we need to approximate the second derivatives in the wave equation by finite differences. One possible way to do that is to use central differences:
\[u_{tt} (x_i, t_n) \approx (u_i^{n+1} - 2 u_i^n + u_i^{n-1}) / dt^2, \qquad u_{xx} (x_i,t_n) \approx (u_{i+1}^n - 2 u_i^n + u_{i-1}^n) / dx^2\]Substituting these approximations into the wave equation and rearranging terms gives:
\[u_i^{n+1} = u_i^n - \frac{cdt}{2dx} (u_{i+1}^n - u_{i-1}^n) + \frac{c^2 dt^2}{2dx^2}(u_{i+1}^n - 2 u_i^n + u_{i-1}^n)\]This formula allows us to compute \(u_i^{n+1}\) from the values of u at time level n and n-1. However, we also need some initial and boundary conditions to start and complete the computation. The initial condition specifies the initial shape of the wave at t=0:
\[u(x,0) = f(x)\]The boundary condition specifies how the wave behaves at the ends of the domain x=0 and x=L:
\[u(0,t) = g(t),\quad u(L,t) = h(t)\]To apply these conditions on the grid, we need to evaluate them at \(x_0=0\) and \(x_{n_x-1}=L\) for all t_n:
\[u_0^n = g(t_n),\quad u_{n_x-1}^n = h(t_n)\]and at all x_i for t_0=0:
\[u_i^0 = f(x_i)\]These values are known from given functions f,g,h or data. Once we have them, we can use them along with the formula above to compute all other values of u on the grid.
Now it is quite clear that although the GPT model has knowledge on the correct formulation of FDM, it failed to perform the task of correctly combining the terms together. This again seems to be part of the flaw of symbolic derivation and computation. The code certainly is elegant, and might well pass for a real “wave equation” solver at first sight, just without the correct physics.